빅오표기법(Big-O notation)

What is bigO notation?

• 알고리즘의 성능을 수학적으로 표현해주는 표기법
• 시간/공간복잡도 표기
• 실제 러닝타임이 아니라 데이터/사용자 증가율에 따른 성능을 예측하는 것이 목표

 

0(1) constant time

F(int[] n){ return (n(0) == 0)? true:false; }

첫번째 배열값이 0인지를 확인, 배열방의 크기에 상관없이 언제나 일정한 속도로 결과를 반환
입력데이터의 크기에 상관없이 constant한 성능이 나오는 함수

 

O(n) linear time

입력데이터의 크기에 비례하여 처리시간이 걸리는 알고리즘

F(int[] n) { for i = 0 to n.length print i }

n의 크기만큼 처리시간이 걸림. 데이터가 들어올 때마다 루프를 돈다.
데이터와 시간이 같은비율로 증가

 

O(n^2) quadratic time

F(int[] n) { for i = 0 to n.length for j = o to n.length print i+j }

n으로 루프를 돌리는데 그 안에서 또 n으로 루프 돌리는 중. 처리횟수는 n을 가로/세로 길이로 가지는 면적만큼 됨.

 

O(nm) quadratic time

F(int[] n, int[] m){ for i = 0 to n.length for j= 0 to m.length print i+j; }

n을 두번 돌리는게 아니라 m을 n만큼 루프

 

O(n^3)

F(int[] n){ for i = 0 to n.length for j = 0 to n.length for k = 0 to n.length print i+j+k }

n으로 삼중루프를 돌아서 n의 세제곱. 즉 큐빅의 모형이 된다. 데이터가 증가하면서 처리시간도 급격히 늘어남.

 

O(2^n) exponbential time

Fibonacci numbers

F(n, r){ if(n <= 0) return 0; else if (n==1) return r[n] = 1; return r[n] = F(n-1, r) + F(n-2, r); }

호출할 때마다 자신앞의 수 2개씩 호출 중. 트리의 높이만큼 반복된다.

O(m^n) exponential time m개씩 n번 늘어나는 알고리즘

 

O(log n) binary search

F(k,arr,s,e) { if(s>e) return -1; m = (s+e) /2; if (arr[m] == k) return m; else if(arr[m] > k) return F(k,arr,s,m-1); else return F(k,arr,m+1,e); }

찾는 값이 중간값보다 작으면 중간값-1, 크다면 중간값+1 하여 한번 호출할 때마다 m 기준으로 절반이 줄어들어 속도도 빠르다. 데이터가 증가해도 성능이 크게 차이나지 않는다.

 

O(Sqrt(n)) square root

맨 위의 한 줄만 돌리면 된다.

 

Check Point

Drop constants. 상수는 무시합니다.
빅오표기법은 실제 알고리즘의 러닝타임을 재는 것이 아니라 처리시간의 증가율을 예측하기 위한 표기법이다.
상수는 고정된 수이므로 증가율에 고정된 상수만큼 영향을 미치기에 신경쓰지 않아도 됨.

F(int[] n) { for i = 0 to n.length print i for i = 0 to n.length print i }

O(2n) -> O(n)

 

Comparing Functions

 

 

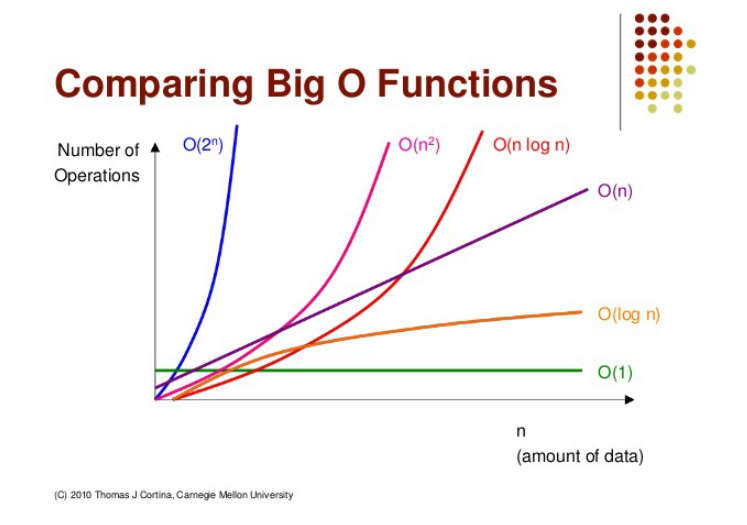
왼쪽에서 오른쪽으로 갈수록 효율성이 떨어진다.

요약 tip

출처
엔지니어대한민국 유투브 , 위키독스
https://noahlogs.tistory.com/27